- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课选自人教A版(2019)必修第二册第9.2.2节,《总体百分位数的估计》,需要1课时完成,本节课是10分钟片段教学,截取了1个课时的一个片段。本节课通过中位数到第80百分位数,再到一般的第p百分位数的探究,以探究栏目提出“居民生活用水定额管理问题”,引出对总体分布的估计问题,以及估计总体分布的途径,而且这个问题贯穿本节始终,通过对该问题的探究,让学生理解一组数据的第p百分位数的概念并掌握求一组数据的百分位数的基本步骤,最后又围绕这个问题的解决方案设计,让学生尝试运用第p百分位数来解决实际问题,体会百分位数的意义和作用,体会用样本估计总体的思想与方法。
依据以上分析,结合学生的实际,确定教学重难点如下:
1.2 教学重点:理解百分位数的概念及其简单应用。
教学难点:求样本数据的第p百分位数。
1.学生已有知识基础
学生在初中已经学习中位数以及统计的初步概念,对样本估计总体有一定的认识。进入高中后,前面已学习过抽样及总体取值规律的相关知识,对用数据、图、表来反映样本的规律有一定的认识,对用数据、列表、绘图等基本方法来解决实际问题的有一定基础。
2.学生学习该内容可能的困难
(1)学生虽然在初中对中位数内容有所学习,但因遗忘等原因,对奇数个样本数据和偶数个样本数据的中位数的求法会产生混淆,再加上更一般的第p百分位数学生并没有接触过,对数据分析缺乏目的性,会引起学生认识上的困惑。如:为什么计算出一组数据百分之p位置不是整数,要取比他大的比邻整数项数据?为什么是整数时,又要取这一项数据与后一项数据的平均值呢?等等。
(2)因缺乏统计思维的训练,学生对统计思想、方法的理解会有一定的困难等。如:为什么能用样本的第p百分位数估计总体?对数据分析,再用来决策于实际问题,对学生会有一定难度等。
依据新课标中的内容与要求,以及学生实际情况,指定教学目标如下:
1.知识与技能目标:
(1)通过实例体会百分位数的意义和作用。
(2)通过实例体会求样本数据的第p百分位数。
(3)通过实例体会第p百分位数的特征,能准确地做出总体估计。
2. 过程与方法目标:
(1)通过对数据的分析为合理决策提供依据,感受统计在现实生活中的作用。
(2)通过对现实生活中的问题的探究,感知应用数学知识解决问题的方法。
3.情感、态度和价值观目标:
通过对样本分析和总体估计的过程,感受数学对实际生活的需要,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系。
教学重点:理解百分位数的概念及其简单应用。
教学难点:求样本数据的第p百分位数。
9.2.2 总体百分位数的估计 1、一组数据的第p百分位数 2、计算一组n个数据的第p百分位数的步骤 |
PPT展示区 |
学生板演区 |
一、创设情境,引入课题
如何求100个数据的中位数?
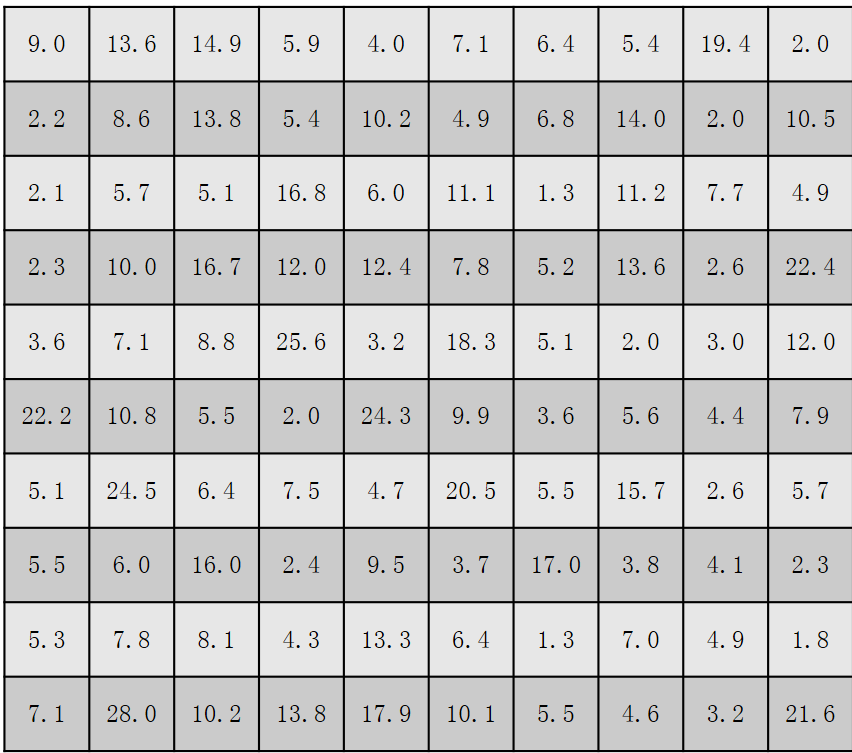
设计意图:学生在初中已经学习了中位数,中位数是第50百分位数。从特殊到一般,符合学情,有利于知识的螺旋上升。
二、提出问题,探求新知
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费。
我们要思考的问题是:
如果该市政府希望使80%的居民用户生活用水费用支出不受影响,你能给市政府提出确定居民用户月均用水标准的建议吗?
(假设通过抽样)我们获得了100位居民某年的月平均用水量(单位:t)
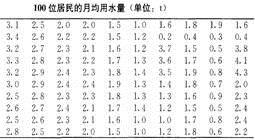
设计意图:由学生身边实例入手,激发学生的学习兴趣,探索热情,特别是问题提出,增加了学生的参与感。也让学生充分体会数学来源于生活,研究统计具有较强的实际意义。
三、操作讨论,探索方法:
用图示展现问题直观含义,找到一个数a,使得不超过a的占80%,超过a的占20%.
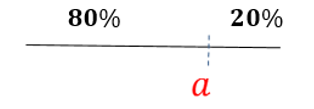
问题:类比中位数的求法,如何求a呢?
具体做法如下:(师生共同探讨)
(1)排序:将100个数据从小到大排列
(2)得到第80个和第81个数据分别为13.6和13.8
问题:直接取第80个数据13.6可以吗?
不可以,不能把100个样本数据分成符合要求的两部分.
但区间(13.6,13.8)内的任意一个数,符合要求.
(3)一般地,我们取第80个数和第81个数的平均数13.7
称13.7为这组数据的第80百分位数或80%分位数
称中位数为第50百分位数或50%分位数
(4) 根据样本数据的第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右. 为了实际中操作的方便,可以建议市政府把全市居民用户月均用水量标准定为14t,或者把年用水量标准定为168t.
设计意图:引导学生把新问题回归到旧知识进行解决,考虑到学生遗忘的因素,先进行展示,唤起学生的记忆,为下一步运用旧知解决问题打下基础。师生共同探讨交流得出结果,能让学生更好地掌握求第P百分位数的步骤,将理论上升为实践,进一步加深对知识的理解。
追问:你认为14t这个标准一定能保证80%的居民用水不超标吗?
不一定。样本数据只是总体数据的一个估计值,抽样方法和样本的随机性都可能导致误差,但这一误差一般不会影响我们对总体分布情况的大致了解。
设计意图:让学生清楚第p百分位的直观意义,通过观察发现规律,为后续内容作好铺垫。
四、定义探究,思考提升
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
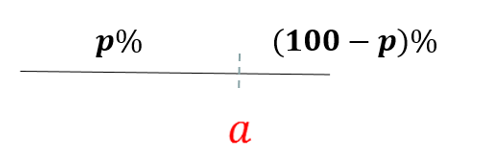
注意: 定义中所有的不等关系都带有等号.
问题:怎么理解等号?
例如问题2中,若第80个数和第81个数相等,平均数就是本身,会出现小于或等于a,大于或等于a的情况。
设计意图:让学生能更进一步地理解一组数据第p百分位数的意义,定义中的不等关系带了等号该怎么理解,学生积极思考,探讨交流,有利于提高学生实际解决问题的能力,让学生体会数学定义的严谨美。
五、巩固练习,深化拓展,提炼方法步骤
例题1 根据某中学高一年级30名男生的体重(单位:kg)样本数据,估计该中学高一年级男生体重的第25,50,75百分位数.

(1)把样本数据按从小到大排序
(2)30个样本数据如何定位到25%的位置?
30×25% =7.5
(3)如何确定最终数据?
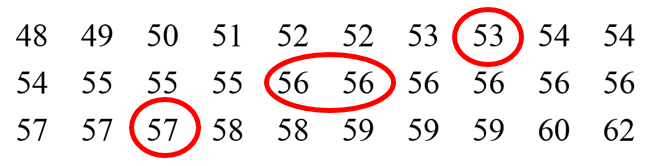
注意:7.5不是整数,在样本数据中找不到对应数据。怎么处理?
举例:若问题2中,n=101,则由80%×101=80.8,取第81个数为80%分位数即可。
补充概念:① 比邻整数 ② 四分位数
方法总结:计算一组n个数据的第p百分位数的步骤:
(1)按从小到大排列原始数据.
(2)计算i=n×p%.
(3)若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
设计意图:师生共同完成第一问,第二问,第三问通过学生的自我实践,熟悉求一组数据的第P百分位数的方法,步骤。同时,也经过学生自己动手来发现操作中的问题。
六、小结反思,提高认识
1.一组数据的第P百分位数:
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2.求一组数据的第p百分位数的基本步骤:
①排序
②指数
③定值(包括指数不是整数;指数是整数两种情况)
(说明:师生共同总结,教师作出提点,通过多媒体一项一项演示出来)
设计意图:小节是一堂课的概括和总结,有利于优化学生的认知结构,把课堂教学传授的知识较快转化为学生的素质,也更进一步培养学生的归纳概括能力。
七、布置作业,独立探究
预习.用频率分布表、频率分布直方图估算百分位数
设计意图:使学生通过作业巩固所学的知识,形成技巧,从而发展为技能。
①判断正误:
(1)若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
(2)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
②根据某中学高一年级30名男生的体重(单位:kg)样本数据,估计该中学高一年级男生体重的第25,50,75百分位数.

老师演示Excel表格中函数“percentile(array,K)”计算百分数的操作流程,学生体会计算机计算结果与自己手动计算结果的区别所在
设为正确答案